La ley de los senos es la relación entre los lados y ángulos de TRIANGULOS no rectángulos (oblicuos). Simplemente, establece que la relación de la longitud de un lado de un triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y ángulos en un triángulo dado.
En TRIGONOMETRIA , el teorema de los senos o también conocido como ley de los senos es una relación de PROPORCIONALIDAD entre las longitudes de los lados de un TRIANGULO y los SENOS de sus respectivos ANGULOS opuestos.
Usualmente se presenta de la siguiente forma:
Teorema de los senosPara usar la ley de los senos necesita conocer ya sea dos ángulos y un lado del triángulo (AAL o ALA) o dos lados y un ángulo opuesto de uno de ellos (LLA). Dese cuenta que para el primero de los dos casos usamos las mismas partes que utilizó para probar la congruencia de triángulos en geometría pero en el segundo caso no podríamos probar los TRIANGULOS CONGRUENTES dadas esas partes. Esto es porque las partes faltantes podrían ser de diferentes tamaños
Si en un triángulo ABC, las medidas de los lados opuestos a los ángulos A, B y C son respectivamente a, b, c, entonces:

La ley de seno es una relación de tres igualdades que siempre se cumplen entre los lados y ángulos de un triángulo cualquiera. En ocasiones necesitarás resolver ejercicios que envuelven triángulos que no son rectángulos. La ley del Seno y la del coseno son muy convenientes para resolver problemas de triángulos en los que no hay ningún ángulo rectángulo como los discutidos en la sección de TRIGONOMETRIA BASICA
Veamos el siguiente triángulo:

Podemos realizar el siguiente procedimiento:
En ΔAMC aplicamos el seno de A y obtenemos y/b = sen A
despejamos para y, obtenemos ------> y= b sen A
En ΔBMC aplicamos el seno de B y obtenemos y/a = sen B
despejamos para y, obtenemos -------> y= a sen B
Igualamos ambas expresiones y=y de forma que: b sen A = a sen B
LEY DE COCENOS
La ley de los cosenos es usada para encontrar las partes faltantes de un TRIANGULO oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la LEY DE LOS SENOS porque no podemos establecer una proporción que pueda resolverse.
La ley de los cosenos establece:
c2 = a2 + b2 – 2abcos C.
Esto se parece al TEOREMA DE PITAGORAS excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos.
La ley de los cosenos también puede establecerse como
b2 = a2 + c2 – 2accos B or
a2 = b2 + c2 – 2bccos A.

El teorema del coseno, denominado también como ley de cosenos , es una generalización del TEOREMAS DE PITAGORAS en los triángulos rectángulos que se utiliza, normalmente, en TRIGONOMETRIA
El teorema relaciona un lado de un triángulo cualquiera con los otros dos y con el COCENO del ANGULO formado por estos dos lados:
Teorema del coseno
Dado un triángulo ABC cualquiera, siendo α, β, γ, los ángulos, y a, b, c, los lados respectivamente opuestos a estos ángulos entonces:

En TRIGONOMETRIA , el coseno (abreviado cos) de un ANGULO agudo en un TRIANGULO RECTANGULO se define como la razón entre el CATETO ADYACENTE a dicho ángulo y la HIPOTENUSA
En virtud del TEOREMA DE TALES , este número no depende del triángulo rectángulo escogido y, por lo tanto, está bien construido y define una FUNCION del ángulo
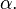
Otro modo de obtener el coseno de un ángulo consiste en representar éste sobre la CIRCUNFERENCIA GIONOMETRIA , es decir, la CIRCUFERENCIA UNITARIA centrada en el ORIGEN . En este caso el valor del coseno coincide con la ABCSICA del punto de intersección del ángulo con la CIRCUFERENCIA . Esta construcción es la que permite obtener el valor del coseno para ángulos no agudos.



No hay comentarios:
Publicar un comentario